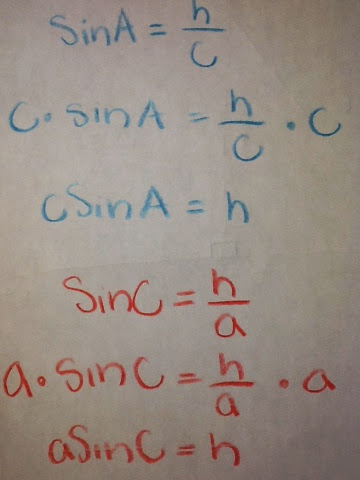SP#7: Unit Q Concept 2: Finding All Trig Functions When Given One Trig Function and Quadrant

This SP8 was made in collaboration with Jennifer Guerrero. Please visit the other awesome posts on their blog by going here.

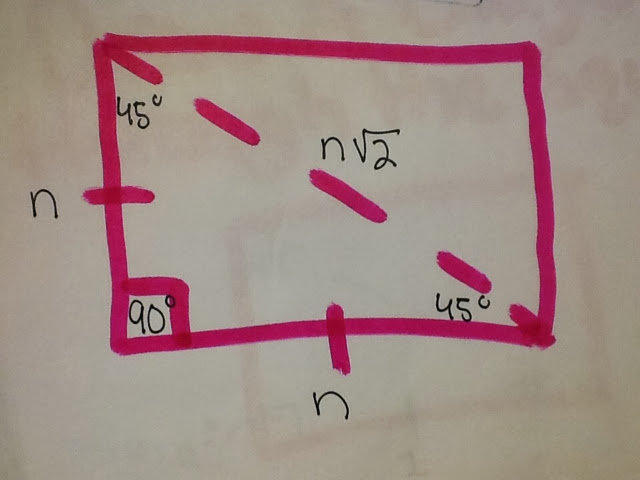
Solving using SOH CAH TOA: 

  

* We used Pythagorean theorem to find the hypotenuse of the triangle.

*making sure to always rationalize a fraction when needed. (ex: cos and sin)

Solving using Identities: 

*we first found what quadrant it lyed on, in order to know which answers were to be positive and which were negative.  (Short cut: All Students Take Calculus)

*we used reciprocal identities to find all but sin. 

* for sin we used a Pythagorean Identity: sin^2x+cos^2x=1

* once again never forgetting to rationalize!!

The viewer needs to pay close attention when solving with identities which ones can be used according to the givens given. Keeping in mind that we can only have one unknone trig function within an identity. Also a key part is never to forget to rationalize! Another thing is that the quadrant it lyes on determines which answers are positive or negative, watch out for the signs. 

I/D #3:Unit Q Concept 1: Using Fundamental Identities to Simplify or Verify Expressions

INQUIRY SUMMARY ACTIVITY

1. Where does sin^2x + cos^2x=1 come from to begin with?

J

An identity is a proven fact and/or formula that is ALWAYS true. The Pythagorean Theorem being itself an identity, as it is a proven statement, that is portrayed in a right triangle within the first quadrant of a unit circle. With using the Pythagorean Theorem, in this case, we use the variables x, y, and r not a^2+b^2= c^2. Instead of it being a, b, and c they would be replaced by x,y,r. 

As worked out in the image above all we had to do to get the Pythagorean Theorem equal to 1 is divide by r^2. By dividing by r^2, we got a ratio used/seen in the unit circle of x/r. Which turns out to be the ratio for cosine.  Another important thing seen is that for the term being added we got y/r, which represents sine when speaking in terms of the unit circle. If we were to substitute those for cos and sin we get: cos^2x + sin^2x = 1. With the substitution we have achieved our Pythagorean identity, through the use of Pythagorean theorem.

I chose one of the "Magic 3" ordered pairs from the unit circle to show that this statement is true. The ordered pair used was the 60* angle, which has coordinates of (1/2, rad3/2).

2. How to derive the two remaining Pythagorean Identities from sin^2x + cos^2x=1

The image above shows that how to derive the identity involving Secant and Tangent. First we have to divide everything by cos^2ø, which would cancel out the cos^2ø making it equal 1. Then we would substitute this ---------> sin^2ø/cos^2ø by tan^2ø. To finish it off we substitute this ---->  1/cos^2ø by this sec^2ø. The answer ending up looking like this: tan^2ø + 1 = sec^2ø. 

In this image the work is shown of how to derive the identity involving Cosecant and Cotangent. The first step taken is dividing everything by sin^2ø. Next we would cancel out sin^2ø and it would be left equal to one. Afterwards we are left with cos^2ø/sin^2ø on one side, what we do with that is substitute it with cot^2ø. Next we would substitute ---> 1/sin^2ø by csc^2ø. Leaving us with our final answer of: 1 + cot^2ø = csc^2ø. 

So now we have been able to tackle the task of deriving each of our three Pythagorean identities. ( tan^2ø + 1 = sec^2ø, 1 + cot^2ø = csc^2ø, and cos^2x + sin^2x = 1) 

WPP #13 & 14: Unit P Concept 6 & 7

Create your own Playlist on LessonPaths!

BQ #1: Unit P Concept 3 and 4: Law of Sines (AAS or ASA) and Area of an Oblique Triangle

Law of sines!

1. Why do we need it? How is it derived from what we already know?

We need the law of sines when working with triangles that are non-right triangles. This is because the normal trig functions are defined for a right triangle not made for non-right triangles. By usiing trig to determine the law of sines we are able to solve for non-right triangles. 

The law of sines is derived by looking at the non-right triangle and creating two right triangles by drawing a line through the middle. Just like in the image below.

Next you would look at some relationships among the triangles. Which would be taking the sin of angle A and C. SinA would be opposite over hypotenuse: h/c. While SinC would be opposite over hypotenuse: h/a. Afterwards you would simply solve for h for both SinA and SinC. This would be done by multiplying by the denominator. For a visual image of this look below.

Now both would end up being equivalent to one another, meaning that both are equal to h. So now you would use the transitive property, setting them equal to one another. Next dividing both sides by  ac, leaving us with the the law of sines! The other relationships may also be derived by dropping perpendicular from the other two vertices. Now we can solve for non-right triangles! 

Area of an oblique triangle!!

2. How is the "area of an oblique" triangle derived? 

The area of an oblique triangle is derived by taking the sinC which is opposite over hypotenuse: h/a. 

Then we would solve for h, by multiplying by the denominator a. Leaving us with aSinC= h. 

Next we would proceed by replacing the h in the original area of a triangle equation with aSinC. 

Leaving us with the equation needed to find the area of an oblique triangle!

A key thing to keep in mind is that there are variations to how the equation is depending on what is given. Also each component of the equation must be different, you can not have angle A and side a in the equation. 

How does it relate to the area formula you are familiar with?

It relates to the area formula I'm familiar with in the way that it comsists of the same basic elements. The only key difference being that height (h) is replaced by the sin of the included angle. 

References: 

 SSS packet 

WPP #12: Unit O Concept 10: Solving angle of elevation and depression word problems

Create your own Playlist on LessonPaths!

I/D #2: Unit O - How can we derive the patterns for our special rights triangle?

Inquiry Activity Summary: 

1.  30-60-90 Triangle 

This is an equilateral triangle from which we will derive a 30-60-90 triangle. In an equilateral triangle all the sides are the same measure and so are the angles. Another thing to keep in mind is that triangles always add up to 180, so we can infer that each of the three angles will be 60*. The first thing to do is split the triangle in half, creating a 90* angle. Another change is that with the split we created a 30* angle. As seen in the image below we have made a 30-60-90 triangle. 

In the image above it's seen how opposite to the 30* angle there is now 1/2, this is because each side length was one and by spliting the triangle in half the bottom side got split in half too. So we know that the side across the 30 degrees is 1/2 and the side across the right angle is 1. Now we will find out what the value of the side across from the 60* angle is by using Pythagorean Theorem. 

The image above demonstrates how to use Pythagorean theorem. Giving us a value for the missing side of radical three divided by two. By now we have successfully derives all the values of the sides of a 30-60-90 triangle. (1/2, 1, and radical 3/2). 

But lastly, so we don't deal with fractions we can multiply each side by 2 in order to get whole numbers. By doing so, side (a) would be 1, side (b) would be radical 3, and side (c) would be 2. Next we go ahead and add the variable of n to all the sides. Now across from 30* angle would be n, across from 60* angle would be n radical 3, and across the 90* angle would be 2n. The reason behind placing the variable n is to show the relationship between the sides, "n" merely just representing any number.

2. 45-45-90 Triangle

Here we have a square with all sides being equal (length of 1), and all angles adding up to 360*,each angle having the same value of 90*. In order to get a 45-45-90 triangle is to draw a diagonal line through the square. As seen in the image below with the split we have acquired 45* angles with the split of the 90* angle. 

Now we know two of our sides and need to find the hypotenuse by using Pythagorean theorem. As seen below after having used Pythagorean theorem the renaming side has a value of radical 2. Now we have derived each of our sides' values ( 1,1,radical 2). 

Finally we need to place "n" into the sides of the triangle. By doing so n takes the place of one, for both sides that have the same value. The remaining side that is across from the 90* angle will be n radical 2. The variable n plays the function of allowing the relationship/ pattern among a 45-45-90 triangle to remain constant, no matter what the value of "n" happens to be.

INQUIRY ACTIVITY REFLECTION

1. SOMETHING I NEVER NOTICED BEFORE ABOUT SPECIAL RIGHT TRIANGLES IS 

that I never really thought that the "n" had a distinct role in special right triangles. I alsways believed it to be just a random variable, but now I see and understand how it helps maintain consistency in relationship among the sides. 

2. BEING ABLE TO DERIVE THESE PATTERNS MYSELF AIDS IN MY LEARNING BECAUSE I can personally figure out the values of the sides if I ever have a brain fart during a test. Not only that, but I now have an a reasonable explanation as to how to get every value of each side.