Law of sines!
We need the law of sines when working with triangles that are non-right triangles. This is because the normal trig functions are defined for a right triangle not made for non-right triangles. By usiing trig to determine the law of sines we are able to solve for non-right triangles.
The law of sines is derived by looking at the non-right triangle and creating two right triangles by drawing a line through the middle. Just like in the image below.
Next you would look at some relationships among the triangles. Which would be taking the sin of angle A and C. SinA would be opposite over hypotenuse: h/c. While SinC would be opposite over hypotenuse: h/a. Afterwards you would simply solve for h for both SinA and SinC. This would be done by multiplying by the denominator. For a visual image of this look below.
Now both would end up being equivalent to one another, meaning that both are equal to h. So now you would use the transitive property, setting them equal to one another. Next dividing both sides by ac, leaving us with the the law of sines! The other relationships may also be derived by dropping perpendicular from the other two vertices. Now we can solve for non-right triangles!
2. How is the "area of an oblique" triangle derived?
The area of an oblique triangle is derived by taking the sinC which is opposite over hypotenuse: h/a.
Then we would solve for h, by multiplying by the denominator a. Leaving us with aSinC= h.
Next we would proceed by replacing the h in the original area of a triangle equation with aSinC.
Leaving us with the equation needed to find the area of an oblique triangle!
A key thing to keep in mind is that there are variations to how the equation is depending on what is given. Also each component of the equation must be different, you can not have angle A and side a in the equation.
It relates to the area formula I'm familiar with in the way that it comsists of the same basic elements. The only key difference being that height (h) is replaced by the sin of the included angle.
References:
SSS packet

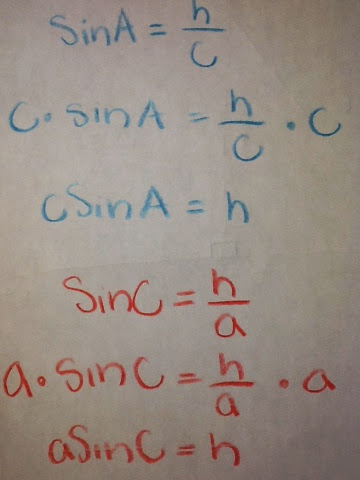






No comments:
Post a Comment