I/D #2: Unit O - How can we derive the patterns for our special rights triangle?

Inquiry Activity Summary: 

1.  30-60-90 Triangle 

This is an equilateral triangle from which we will derive a 30-60-90 triangle. In an equilateral triangle all the sides are the same measure and so are the angles. Another thing to keep in mind is that triangles always add up to 180, so we can infer that each of the three angles will be 60*. The first thing to do is split the triangle in half, creating a 90* angle. Another change is that with the split we created a 30* angle. As seen in the image below we have made a 30-60-90 triangle. 

In the image above it's seen how opposite to the 30* angle there is now 1/2, this is because each side length was one and by spliting the triangle in half the bottom side got split in half too. So we know that the side across the 30 degrees is 1/2 and the side across the right angle is 1. Now we will find out what the value of the side across from the 60* angle is by using Pythagorean Theorem. 

The image above demonstrates how to use Pythagorean theorem. Giving us a value for the missing side of radical three divided by two. By now we have successfully derives all the values of the sides of a 30-60-90 triangle. (1/2, 1, and radical 3/2). 

But lastly, so we don't deal with fractions we can multiply each side by 2 in order to get whole numbers. By doing so, side (a) would be 1, side (b) would be radical 3, and side (c) would be 2. Next we go ahead and add the variable of n to all the sides. Now across from 30* angle would be n, across from 60* angle would be n radical 3, and across the 90* angle would be 2n. The reason behind placing the variable n is to show the relationship between the sides, "n" merely just representing any number.

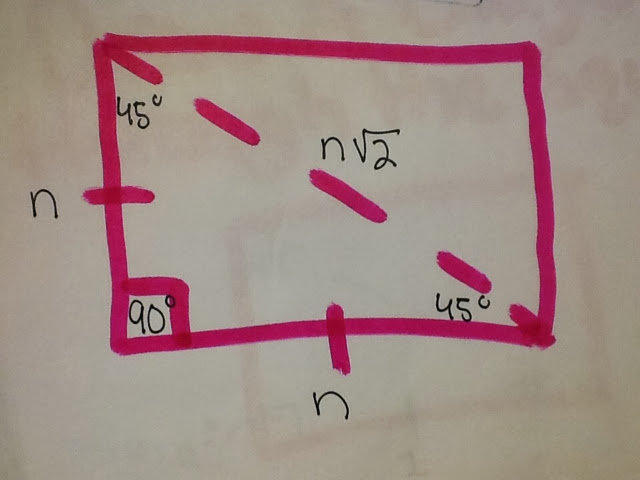
2. 45-45-90 Triangle

Here we have a square with all sides being equal (length of 1), and all angles adding up to 360*,each angle having the same value of 90*. In order to get a 45-45-90 triangle is to draw a diagonal line through the square. As seen in the image below with the split we have acquired 45* angles with the split of the 90* angle. 

Now we know two of our sides and need to find the hypotenuse by using Pythagorean theorem. As seen below after having used Pythagorean theorem the renaming side has a value of radical 2. Now we have derived each of our sides' values ( 1,1,radical 2). 

Finally we need to place "n" into the sides of the triangle. By doing so n takes the place of one, for both sides that have the same value. The remaining side that is across from the 90* angle will be n radical 2. The variable n plays the function of allowing the relationship/ pattern among a 45-45-90 triangle to remain constant, no matter what the value of "n" happens to be.

INQUIRY ACTIVITY REFLECTION

1. SOMETHING I NEVER NOTICED BEFORE ABOUT SPECIAL RIGHT TRIANGLES IS 

that I never really thought that the "n" had a distinct role in special right triangles. I alsways believed it to be just a random variable, but now I see and understand how it helps maintain consistency in relationship among the sides. 

2. BEING ABLE TO DERIVE THESE PATTERNS MYSELF AIDS IN MY LEARNING BECAUSE I can personally figure out the values of the sides if I ever have a brain fart during a test. Not only that, but I now have an a reasonable explanation as to how to get every value of each side.