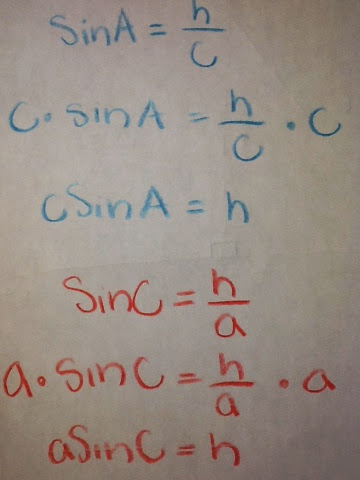BQ #7

The formula for the difference quotient is f(x+h)- f(x) divided by h. It is derived from the slope formula of y^2-y^1/x^2-X^1. The only difference is that as seen on the graph the section of x+h is substituted  in the place of y^2 and then y with x. Next its done the same with the bottom leaving it as x+h-x. Next you move on by canceling out the x's leaving the h on the bottom. So its simply substituting in the correct values into the slope formula resulting in the difference quotient. This all being shown in the image provided. The image shows how delta x can be used as another notation for the h. The purpose always being to get delta x as small as possible, making the tangent line less steep. Because the smaller the delta x, the more the secant and tangent lines resemble one another.

BQ #6: Unit U

1. What is continuity? What is discontinuity?

A continuity is a continuous function that is predictable has no holes, no breaks, and no jumps. You can also draw it without lifting your pencil from the paper. Another key characteristic is that the value equals the limit. An example of a continuous function would be this below: 

(Mrs.kirch)

A discontinuity is the complete opposite to that of a continuous function. There are two groups of discontinuities: the non-removable and removable discontinuities. A point discontinuity involves the graph having a hole, meaning that limit does exist but because of the hole the value is undefined. But if there were to be a black dot below it or underneath it that would give us the value. A point discontinuity is within the removable discontinuity. Moving onto the non-removal discontinuities the first one is called a jump discontinuity in which involves different left right endings, end in different locations.It's important  to keep in mind that both circles cannot be closed or it is not a function, also if both circles are open the value of the function is undefined. The next type is an oscillating discontinuity which is basically a wiggly graph, and is rarely seen. The last type would be infinite discontinuity which because of the vertical asymptote the graph exhibits unbounded behavior. Unbounded behavior simply meaning that increases or decreases without bound. Each one clearly portrayed in the image below:

(Mrs. Kirch)

2. What is a limit? When does a limit exist/not exist? What is the difference between a limit and a value? 

A limit is the intended height of a function. A limit does not exist when dealing with the three non-removable discontinuities: jump, oscillating, and infinite. In a jump discontinuity the limit would not exist because both lines do not meet at same place (an intended limit). This is seen when we evaluate the limit by placing our fingers on a spot to the left and to the right of where we want to evaluate the limit, if our fingers do not meet our limit does not exist. The next type would be infinite discontinuity in which the limit does not exist because of unbounded behavior, but value does exist at one value end of the one sided limits. The last type being an oscillating discontinuity in which limit does not exist because of oscillating behavior. A limit does exist when dealing with a continuous funvtion because the limit and the value equals one another. A limit is the intended height of the function and value is the actual height of a function (where black dot lies).

The image below shows limits in which the limit/values that do or do not exist:

(Mrs. Kirch)

3. How do we evaluate limits numerically, graphically, and algebraically? 

 We evaluate limits numeracally on a table shows how we gradually get closer and closer to a limit and value. This is done by making a table and at center placing the limit to get the limit from left we subtract 1/10 and to get limit from right you add 1/10. And to find the values we plug the function into our calculators and trace for value we are looking for. Next graphically is finding the limit bases on use of graphing calculator by typing in function, going to graph, hitting trace, and just tracing for the value we want. Or by being given a graph in which we simply evaluate the limit by placing our finger on a spot left and to the right of where you want to evaluate the limit. When it comes to algebraically we use three different forms: direct substitution, dividing out/factoring method, and rationalizing/conjugate method. Direct substitution involves plugging in the number x is approaching, and if it results in a numerical answer you are done, if it results in 0/# answer is zero and you are done, if we get #/0 then it's undefined meaning limit does not exist (here we must state a reason as to why doesn't exist), if we get 0/0 it's un determinate form meaning we have to use another method. Another method like the dividing out/factoring in which we factor both the numerator and denominator and cancel common terms to remove the zero in the denominator, then proceed by using direct substitution with the simplified expression. The other method is known as rationalizing/conjugate in which: if it's a fraction we multiply by the conjugate  ( only the sign in the middle of both terms changes), depending where the radical is you take the conjugate of where it is, that either being in the numerator or denominator. Then we simplify by foiling, leaving the non-conjugated denominator or numerator factored. Next proceeding by canceling out like terms, leaving us with a simplified expression. Finally using direct substitution with the simplified expression. One huge thing to always do is to try direct substitution first, and if doesn't work out proceed with the other two methods.

BQ#4 – Unit T Concept 3

Why is a “normal” tangent graph uphill, but a “normal” cotangent graph downhill? Use unit circle ratios to explain.

The normal tangent graph is up hill because its ratio consists of (sin/cos): y/x. That meaning that when x is equal to zero the ratio is made undefined. By referring back to the unit circle we can see that x equals zero at pi/2 and 3pi/2, meaning that that is were our asymptotes lye for tangent. Meaning that the graph has to be within those two boundaries. Another thing to keep in mind is that tangent consists of a pattern of positive, negative, positive, negative, depending on what quadrants the graph lys in tells u whether it is up sloping or down sloping. As seen in the image below normal tangent graph is uphill because of where it's boundaries were.

When taking a look at cotangent we first see what ratio it has which is the complete opposite to that of tangent: cos/ sin, x/y. with that we can now refer back to our unit circle and see where y/sin equals zero, because that is where our assymptotes will be. Sine is zero at zero and pi, as you can tell our boundaries are now different, making us fall into different quadrant. Because of that changing the complete look of the graph, making it into a  down sloping graph. Although some part did remain the same which was the pattern of positive, negative, positive,negative.

BQ#3 – Unit T Concepts 1-3

How do the graphs of sine and cosine relate to each of the others?  Emphasize asymptotes in your response.

1. Tangent
        In the first quadrant (shaded red) you can tell that the cosine values in green and the sine values in red, are all positive because they are above the x-axis.  Since all trig values are positive in the first quadrant we can infer that tan (the orange line) will be and is positive within this quadrant. In the second quadrant cosine is negative (green line) and sine is positive (red line) and with the tan ratio being: tan(x)=sin(x)/cos(x), it leaves us with a positive divided by a negative, which we get a product of a negative value. That being why in this quadrant the tangent values fall below the x-axis. When looking at our third quadrant we can see that our cos and sine values are both below the x-axis meaning their negative, once again making tangent positive because negative divided by negative gives you a positive. The same goes on in the fourth quadrant as cos is positive and sine is negative giving us a tan of negative. Now when we look at the asymptotes involved with such trig functions by looking at our ratio identity for tan= sin/cos and see that cosine must equal 0 in order to get an undefined value. We get cosine to equal zero by looking at the unit circle pointing out those x-values in which there is a zero, those coordinates being (0,1) which is pi and (0, -1) in other words 3pi/2. Those spots being where our tangent graph seems as if to stop, that is because they are our asymptotes. As noticed a difference being that tan involves assymptotes unlike sin and cos. 

(Mrs. Kirch creation on desmos)

2. Cotangent
   With Cotangent having a ratio of cos/sin, the values of cos and sin affect where cotangent will lye whether below or above the x-axis. This was the same case when dealing with tangent, it's only going to be the opposite. As the asymptotes are located at 0 and 180 because y=0, as you can see we look at the y value this time not x. By using the trig ratio for cot (cos/sin) if both Sin and cos where to be positive in the first quadrant ( red ), we get a positive value for cot. When in quadrant 2 (green) we get a negative value for cot, because we positive/ negative. For the third quadrant (orange) we get a positive value for cot, positive/positive. In  the fourth quadrant (blue),we get a negative value for cot because it's a  Positive/negative. The graph for cotangent holding a pattern that is positive, negative, positive, negative as seen in the image above. The only times we see it break up is at the asymptotes that lye on 0 and 180.

(Mrs. Kirch creation on desmos)

3. Secant
    When looking at secant and the relationship it holds among cosine and sine is that it's the reciprocal of cosine, having a ratio of 1/cos. With cosine being the denominator, when it does equal a zero making the ratio undefined we get a assymptotes. When looking at the unit circle cosine equals zero at (90*) pi/2 and 3pi/2 (270*). By looking at the graph it's seen how when cosine is positive so shall the secant be positive, and when negative it will be negative.

(Mrs. Kirch creation on desmos)
4. Cosecant
     The relationship that Cosecant has with sine and cosine is that it is the reciprocal of sine, having a ratio of 1 over sine. With sine being the denominator  when it is zero it makes the ratio undefined giving us an asymptote. When taking a look at the unit circle, the ones with a zero on the x is zero and pi, meaning that Cosecant has asymptotes at 0 and pi. As seen in the graph when sine is positive so will the cosecant graph.  Same goes when sine is negative, sine controlling whether the cosecant graph goes up hill or down hill.

• (Mrs. Kirch creation on desmos)

* as noticed in all of the graphs dealing with asymptotes the line never crosses or touches the asymptote. Always by it never through it. As seen in the image above csc line in red just goes beside it.

BQ#5 – Unit T Concepts 1-3

1) Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

When looking at the ratios of both cosine and sine you notice that both ratios are over r. As cosine is equal to y/r and sine is equal to x/r, since the radius, which will always be one, it means that you will never have zero as a denominator. If there is no zero in the denominator to make it undefined, then there will never be any asymptotes. For, asymptotes= undefined. When for the rest of te other trig graphs of cosecant, secant, cotangent, and tangent all have the possibility of the ratio having a zero as a denominator, thus making it undefined. And when it's undefined that only means one thing that it does have asymptotes. 

BQ #2: Unit T Concept Intro

How do the trig graphs relate to the Unit Circle?

The trig graphs belive it or not relate to the unit circle in a big way. One period of a trig graph is one full revolution of the unit circle, no matter what. The trig graph relating to the Unit Circle in the way that it  indicates when the trig graph is negative (down sloping) or positive (up sloping). For example; when looking at sine in terms of the unit circle it's pattern is positive, positive, negative, negative. This means that everytime it goes through one cycle while covering 2pi units on the x-axis. That is as to why the sine trig graph looks the way it does. Same situation applies to cosine, cosecant, and secant. Cosine's pattern being: positive, negative, negative, and positive. Although the only exception is tangent/cotangent who instead goes through one cycle covering pi units on the x-axis. Tangents pattern being: positive, negative, positive, negative.

Period? - Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

-The period for a sine and cosine covers 2pi units on the x axis, because as seen in the image above in the sine pattern that goes positive, positive negative, negative. Which means it goes up slopping, up sloping, down slope, down slope and because of that it doesn't cross the x axis till 2pi. Same going for cosine.

While for tangent/cotangent it covers pi units on the axis, because again as seen in the image above the tan pattern is positive, negative, positive, negative. Meaning that it goes up slope, down slope, up slope, and down slope which gives us have a more squished graph. Unlike the sine and cosine graph which appears to be a bit more apart.

Amplitude? – How does the fact that sine and cosine have amplitudes of one (and the other trig functions don’t have amplitudes) relate to what we know about the Unit Circle?

Sine and cosine have amplitudes of one because when referring to the ratios of each sine has a ratio of y/r and cosine has ratio of x/r. R being the radius of the unit circle, which is 1. That is as to why sine and cosine can be no larger than one or negative one, as said so in past units. But when dealing with other trig functions and the ratios they have the same doesn't apply to them. For instance tangent has a ratio of y/x meaning that we no longer are dividing by one, instead we dividing by different numbers, thus getting different values. The same thing applying to cotangent, who has a ratio of x/y. This also applies to csc with ratio of r/y and sec with ratio of r/x. Which can be divisible by fractions, and proceeding by multiplying with the reciprical of the denominator.

Reflection #1 - Unit Q: Verifying Trig Identities

24. What does it actually mean to verify a trig function? 

It's basically when you are given a trig function and you know what the answer is. All that is needed to be done is for you to work with the trig function given on the left side and get the answer that lyes on the right.You verify to see if the statement is true, that the trig function actually equals that answer. One thing that you must keep in mind is to always work with the messy side, leaving the right side alone, throughout the whole problem.

25.What tips and tricks have you found helpful?

A big tip that proves to be very helpful is to have the identities memorized, or at least have them at hand whenever working with a problem. Also you may never divide by trig, instead when tempted move everything to the side and pull out a GCF. Another tip is that when squaring both sides, you should check for any extraneous solution. One other thing is that you multiply by the conjugate only when the denominator is a binomial. When denominator is a monomial you can proceed by separating into seperate fractions. Lastly when all fails, try converting all terms to sines and cosines.

26. Explain your thought process and steps you take in verifying a trig identity. Do not use a specific example, but speak in general terms of what you would do no matter what they give you.

When presented with a trig function I see as to whether I need to verify it or simplify it. If it does happen to be a verifying problem I leave the right side alone. Moving on by working with what I am given. Looking for anything I can substitute with an identity, if there's nothing I proceed by taking a look at the denominators. If the denominator is a monomial I seperate the trig function into two seperate fractions, or if it's a binomial I multiply by the conjugate. Afterwards substituting or foiling out what I'm left with, making my way through the problem to achieve what I want, either being a simplified or verified answer.

SP#7: Unit Q Concept 2: Finding All Trig Functions When Given One Trig Function and Quadrant

This SP8 was made in collaboration with Jennifer Guerrero. Please visit the other awesome posts on their blog by going here.

Solving using SOH CAH TOA: 

  

* We used Pythagorean theorem to find the hypotenuse of the triangle.

*making sure to always rationalize a fraction when needed. (ex: cos and sin)

Solving using Identities: 

*we first found what quadrant it lyed on, in order to know which answers were to be positive and which were negative.  (Short cut: All Students Take Calculus)

*we used reciprocal identities to find all but sin. 

* for sin we used a Pythagorean Identity: sin^2x+cos^2x=1

* once again never forgetting to rationalize!!

The viewer needs to pay close attention when solving with identities which ones can be used according to the givens given. Keeping in mind that we can only have one unknone trig function within an identity. Also a key part is never to forget to rationalize! Another thing is that the quadrant it lyes on determines which answers are positive or negative, watch out for the signs. 

I/D #3:Unit Q Concept 1: Using Fundamental Identities to Simplify or Verify Expressions

INQUIRY SUMMARY ACTIVITY

1. Where does sin^2x + cos^2x=1 come from to begin with?

J

An identity is a proven fact and/or formula that is ALWAYS true. The Pythagorean Theorem being itself an identity, as it is a proven statement, that is portrayed in a right triangle within the first quadrant of a unit circle. With using the Pythagorean Theorem, in this case, we use the variables x, y, and r not a^2+b^2= c^2. Instead of it being a, b, and c they would be replaced by x,y,r. 

As worked out in the image above all we had to do to get the Pythagorean Theorem equal to 1 is divide by r^2. By dividing by r^2, we got a ratio used/seen in the unit circle of x/r. Which turns out to be the ratio for cosine.  Another important thing seen is that for the term being added we got y/r, which represents sine when speaking in terms of the unit circle. If we were to substitute those for cos and sin we get: cos^2x + sin^2x = 1. With the substitution we have achieved our Pythagorean identity, through the use of Pythagorean theorem.

I chose one of the "Magic 3" ordered pairs from the unit circle to show that this statement is true. The ordered pair used was the 60* angle, which has coordinates of (1/2, rad3/2).

2. How to derive the two remaining Pythagorean Identities from sin^2x + cos^2x=1

The image above shows that how to derive the identity involving Secant and Tangent. First we have to divide everything by cos^2ø, which would cancel out the cos^2ø making it equal 1. Then we would substitute this ---------> sin^2ø/cos^2ø by tan^2ø. To finish it off we substitute this ---->  1/cos^2ø by this sec^2ø. The answer ending up looking like this: tan^2ø + 1 = sec^2ø. 

In this image the work is shown of how to derive the identity involving Cosecant and Cotangent. The first step taken is dividing everything by sin^2ø. Next we would cancel out sin^2ø and it would be left equal to one. Afterwards we are left with cos^2ø/sin^2ø on one side, what we do with that is substitute it with cot^2ø. Next we would substitute ---> 1/sin^2ø by csc^2ø. Leaving us with our final answer of: 1 + cot^2ø = csc^2ø. 

So now we have been able to tackle the task of deriving each of our three Pythagorean identities. ( tan^2ø + 1 = sec^2ø, 1 + cot^2ø = csc^2ø, and cos^2x + sin^2x = 1) 

WPP #13 & 14: Unit P Concept 6 & 7

Create your own Playlist on LessonPaths!

BQ #1: Unit P Concept 3 and 4: Law of Sines (AAS or ASA) and Area of an Oblique Triangle

Law of sines!

1. Why do we need it? How is it derived from what we already know?

We need the law of sines when working with triangles that are non-right triangles. This is because the normal trig functions are defined for a right triangle not made for non-right triangles. By usiing trig to determine the law of sines we are able to solve for non-right triangles. 

The law of sines is derived by looking at the non-right triangle and creating two right triangles by drawing a line through the middle. Just like in the image below.

Next you would look at some relationships among the triangles. Which would be taking the sin of angle A and C. SinA would be opposite over hypotenuse: h/c. While SinC would be opposite over hypotenuse: h/a. Afterwards you would simply solve for h for both SinA and SinC. This would be done by multiplying by the denominator. For a visual image of this look below.

Now both would end up being equivalent to one another, meaning that both are equal to h. So now you would use the transitive property, setting them equal to one another. Next dividing both sides by  ac, leaving us with the the law of sines! The other relationships may also be derived by dropping perpendicular from the other two vertices. Now we can solve for non-right triangles! 

Area of an oblique triangle!!

2. How is the "area of an oblique" triangle derived? 

The area of an oblique triangle is derived by taking the sinC which is opposite over hypotenuse: h/a. 

Then we would solve for h, by multiplying by the denominator a. Leaving us with aSinC= h. 

Next we would proceed by replacing the h in the original area of a triangle equation with aSinC. 

Leaving us with the equation needed to find the area of an oblique triangle!

A key thing to keep in mind is that there are variations to how the equation is depending on what is given. Also each component of the equation must be different, you can not have angle A and side a in the equation. 

How does it relate to the area formula you are familiar with?

It relates to the area formula I'm familiar with in the way that it comsists of the same basic elements. The only key difference being that height (h) is replaced by the sin of the included angle. 

References: 

 SSS packet 

WPP #12: Unit O Concept 10: Solving angle of elevation and depression word problems

Create your own Playlist on LessonPaths!

I/D #2: Unit O - How can we derive the patterns for our special rights triangle?

Inquiry Activity Summary: 

1.  30-60-90 Triangle 

This is an equilateral triangle from which we will derive a 30-60-90 triangle. In an equilateral triangle all the sides are the same measure and so are the angles. Another thing to keep in mind is that triangles always add up to 180, so we can infer that each of the three angles will be 60*. The first thing to do is split the triangle in half, creating a 90* angle. Another change is that with the split we created a 30* angle. As seen in the image below we have made a 30-60-90 triangle. 

In the image above it's seen how opposite to the 30* angle there is now 1/2, this is because each side length was one and by spliting the triangle in half the bottom side got split in half too. So we know that the side across the 30 degrees is 1/2 and the side across the right angle is 1. Now we will find out what the value of the side across from the 60* angle is by using Pythagorean Theorem. 

The image above demonstrates how to use Pythagorean theorem. Giving us a value for the missing side of radical three divided by two. By now we have successfully derives all the values of the sides of a 30-60-90 triangle. (1/2, 1, and radical 3/2). 

But lastly, so we don't deal with fractions we can multiply each side by 2 in order to get whole numbers. By doing so, side (a) would be 1, side (b) would be radical 3, and side (c) would be 2. Next we go ahead and add the variable of n to all the sides. Now across from 30* angle would be n, across from 60* angle would be n radical 3, and across the 90* angle would be 2n. The reason behind placing the variable n is to show the relationship between the sides, "n" merely just representing any number.

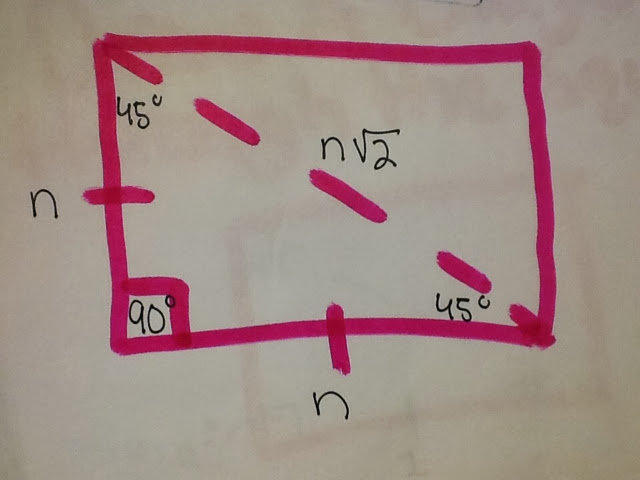
2. 45-45-90 Triangle

Here we have a square with all sides being equal (length of 1), and all angles adding up to 360*,each angle having the same value of 90*. In order to get a 45-45-90 triangle is to draw a diagonal line through the square. As seen in the image below with the split we have acquired 45* angles with the split of the 90* angle. 

Now we know two of our sides and need to find the hypotenuse by using Pythagorean theorem. As seen below after having used Pythagorean theorem the renaming side has a value of radical 2. Now we have derived each of our sides' values ( 1,1,radical 2). 

Finally we need to place "n" into the sides of the triangle. By doing so n takes the place of one, for both sides that have the same value. The remaining side that is across from the 90* angle will be n radical 2. The variable n plays the function of allowing the relationship/ pattern among a 45-45-90 triangle to remain constant, no matter what the value of "n" happens to be.

INQUIRY ACTIVITY REFLECTION

1. SOMETHING I NEVER NOTICED BEFORE ABOUT SPECIAL RIGHT TRIANGLES IS 

that I never really thought that the "n" had a distinct role in special right triangles. I alsways believed it to be just a random variable, but now I see and understand how it helps maintain consistency in relationship among the sides. 

2. BEING ABLE TO DERIVE THESE PATTERNS MYSELF AIDS IN MY LEARNING BECAUSE I can personally figure out the values of the sides if I ever have a brain fart during a test. Not only that, but I now have an a reasonable explanation as to how to get every value of each side.

I/D 1: Unit: N- How do SRT and UC relate?

A)

Here we are dealing with a 30* angle in which the horizontal side is x radical 3, the vertical side x, hypotenuse 2x. We start of by dividing everything by 2x because we need hypotenuse to be one. After canceling out the x we are left with a vertical side of 1/2, horizontal side of radical 3/2, and hypotenuse of one. Afterwards we plot it on the first quadrant deriving the ordered pairs of (radical 3/2,1/2), (radical 3/2,0), and (0,0) as the center. 

B) 

This triangle is a 45* angle and the labeling of the sides differs than those of the 30* angle. Here both the vertical and horizontal side are radical 2/2 and the hypotenuse is 1. We the just plot it on the first quadrant and get the ordered pairs of (0,0), (radical 2/2,0), (radical 2/2, radical 2/2). 

C) 

This is a 60* angle and it is similar to the 30* angle it's just that the sides are switched around. The hypotenuse still being 2x, the vertical side x radical 3, and the horizontal side as x. We first divide everything by 2x and we get a vertical side of radical 3/2, a horizontal side of 1/2, and hypotenuse of one. Next we place the triangle on the first quadrant giving us ordered pairs of (1/2, radical 3\2), (1/2,0), and (0,0). 

This activity helps me derive the unit circle by allowing me to know the ordered pair of a 30*, 45*, and a 60* angle. Which are the basic three triangle used in the entire unit circle. By drawing triangles on the first quadrant we get the positive ordered pairs. When triangles plotted on the 2nd quadrant ordered pairs would have a negative x value. When in the 3rd quadrant both x and y would have a negative values. When in the last quadrant (4) the y value will be negative. Other bottom image shows how the triangles are just flipped around depending on the quadrant it's in. 

 

1. THE COOLEST THING I LEARNED FROM THIS ACTIVITY WAS: that the unit circle primarily consists of these three triangles a 30*, 45*, and a 60*. That they only get flipped around depending on the quadrant they are in. 
2. THIS ACTIVITY WILL HELP ME IN THIS UNIT BECAUSE: it's another way to find the ordered pairs in the unit circle. So in case I forget one of them I can use this tool  to help me find the ordered pair. 
3. SOMETHING I NEVER REALIZED BEFORE ABOUT SPECIAL RIGHT TRIANGLES AND THE UNIT CIRCLE IS:  something that I had not realized about right triangles is that they played an important part I. The unit circle. And something that the unit cicle has is that it involves same points just switched around depending on the quadrant. 

RWA1: Unit M Concepts 4-6 : Conic Sections in real life.

Parabola

1. Mathematical Definition: "Any point on a parabola is at an equal distance from a fixed point (the focus), and a fixed straight line (the directrix)" (Math is fun)."

2. Conic Section:  

A) Algebraically             

http://www.algebra-online.com/tutorials-4/algebra-formulas/articles_imgs/7976/formul92.jpg 

B) Graphically

http://www.clausentech.com/lchs/dclausen/algebra2/lecture_notes/conics/vertical_parabola.jpg

B)  Graphically                                                                                 

http://www.clausentech.com/lchs/dclausen/algebra2/lecture_notes/conics/horizontal_parabola.jpg

The parabola comes with several key features: vertex, directrix, focus, and the axis of symmetry. The vertex is the point at which the parabola starts. The directrix is a line outside the parabola, perpendicular to the axis of symmetry. The axis of symmetry is a line that breaks the graph into two equal halves. The focus is the point inside the parabola. Lastly the "p" is the distance between the directrix and the focus and the from the focus to the vertex. All of which contribute to graphing a parabola accurately. 

Each of those parts can be derived from a general equation like 2y^2+x+24y+75=0, taking the first step which would be to turn it into standard form. This being done so by completing the square, remembering to there needs to be something squared on one side and a coefficient on the other. Once the equation is in standard form the key parts can be discovered. The vertex is (h,k), the "p" is the coefficient set equal to 4p, and from looking at the "p" and the equation you can tell whether it opens up, right, down or left. If "p" is positive and the equation is x^2 goes up, if "p" is positive and equation is y^2 goes right, if "p" is negative and equation is x^2 opens down, if "p" is negative and the equation is y^2 the graph opens left. With "p" being small (closer to vertex) it makes the parabola skinny, if its bigger (farther from vertex)  the parabola is fatter. Then you find both the directrix and focus by counting away from the vertex by the value of "p". Then there's the axis of symmetry which is perpendicular to the directrix and passes through the vertex. Lastly, the eccentricity of a parabola should be equal to one. To visually see this worked out you can seek HERE for more assistance.

3. Real World Application:

http://www.jamesburgdish.org/LinkClick.aspx?link=IBA-4_elevation.JPG&tabid=524&mid=998

A Satellite dish is the perfect example of a real life application of a parabola. The actual dish capturing the actual figure of a parabola. Thus creating an effect that causes waves that come in toward the dish to reflect off of it. And as the waves are reflected they bounce their way to the sphere (receiver) which in this case is the focus point of the parabola. With that it allows for their to be better signal and efficient cable. 

The satellite itself is the parabola with a focus as the main point. That is the spot at which all the waves end up going no matter where the waves hit on the  dish. This could serve to represent the "p" show the distance between the directrix and vertex is equal to the distance from the focus and vertex. How its an  equal distance from any given point, explaining as to why the waves all end up hitting the focus. Another thing would be that in small dishes the focus would have to be closer to the vertex and in a large dish it would be farther. 

4. References:

http://www.mathsisfun.com/definitions/parabola.html

http://bit.ly/zbruh4

https://www.google.com/search?q=parabola